최소 공통 조상

최소 공통 조상

영어로 Lowest Common Ancestor(LCA)라고도 불리는 이 알고리즘은 영어 해석 그대로 최소 공통 조상을 찾는 알고리즘이다.

이를 풀어서 해석해보자면, 두 정점 u,v에서 가장 가까운 공통 조상을 찾는 과정을 말한다.

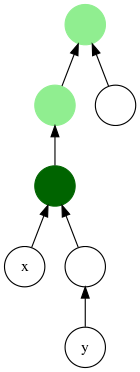
위의 그래프를 보면 LCA(x, y)는 진한 초록색이라고 볼 수 있다.

연한 녹색은 x,y의 공통 조상이기는 하지만 최소는 아니라고 볼 수 있다.

구현 방식의 종류

구현 방법은 크게 세그먼트 트리 방식과 dp 방식이 있다. 아직 세그먼트리는 배우지 않았으니 여기서는 dp과정만 배워보도록 하겠다.

세그먼트 트리를 활용한 구현방법이 궁금한 사람을 위해 링크를 붙여 놓도록 하겠다.

참고로 두 가지 알고리즘 모두 시간복잡도가 동일하다. 자세한 시간 복잡도는 dp 알고리즘을 구현하며 소개해보도록 하겠다.

LCA 알고리즘의 구현

기본적으로 LCA 순서는 다음과 같다.

1. 모든 노드에 대한 깊이를 계산한다.
2. 최소 공통 조상을 찾을 두 노드를 확인한다.
   1. 먼저 두 노드의 깊이가 동일하도록 거슬러 올라간다.
   2. 이후에 부모가 같아질 때까지 반복적으로 두 노드의 부모 방향으로 거슬러 올라간다.
3. 모든 LCA(a, b)연산에 대하여 2번 과정을 반복한다.

이 과정을 그림으로 예를 들어가며 보도록 하자.

1. 먼저 아래와 같이 8번 노드와 15번 노드의 공통 조상을 찾아야 하는 상황이라고 가정해보자

   

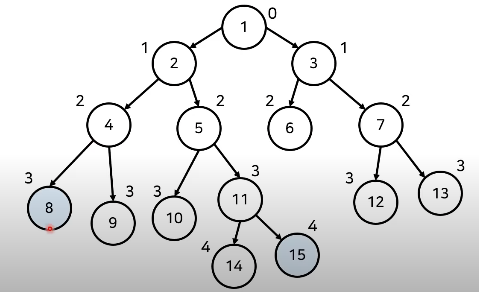
2. 이제 두 노드의 깊이를 맞춰 준다. 15가 8보다 높이가 1이 더 낮으므로 11로 올려 높이를 맞춘다.

   

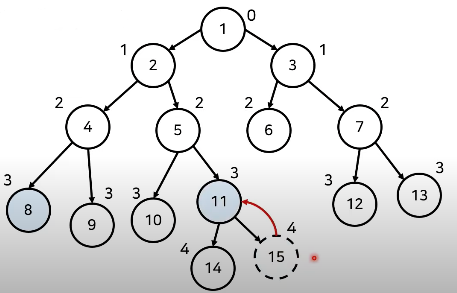
3. 노드의 높이를 올라가며 공통된 조상을 찾는다.

   

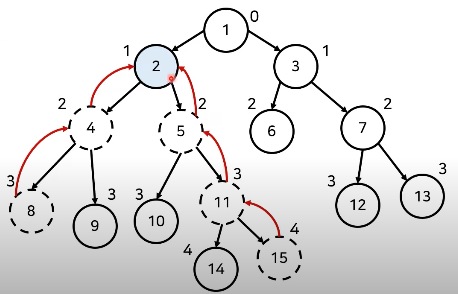
이렇게 매 쿼리마다 부모 방향으로 거슬러 올라가면 최악의 경우 $O(N)$의 시간복잡도가 요구된다. 따라서 모든 쿼리M개를 처리할 때의 시간 복잡도는 $O(NM)$이다.

tip

여기서 N은 트리의 높이를 의미합니다.

이것을 좀더 효율적으로 처리하기 위해 사용하는 것이 dp이다. dp를 사용하면 부모 방향으로 거슬러 올라가는 시간복잡도를 $O(logN)$으로 줄일 수 있다.

기존의 거슬러 올라가는 노드의 속도를 한칸씩 올라갔다면 dp를 사용하여 $2^n$속도로 올라갈 수 있다.

예를 들어, 총 15칸 올라가야 한다면 8칸 -> 4칸 -> 2칸 -> 1칸 이런식으로 올라가는 것이다. 아래 그림 처럼 dp배열에 $2^i$ 번째 조상의 노드를 기록해두면 된다.

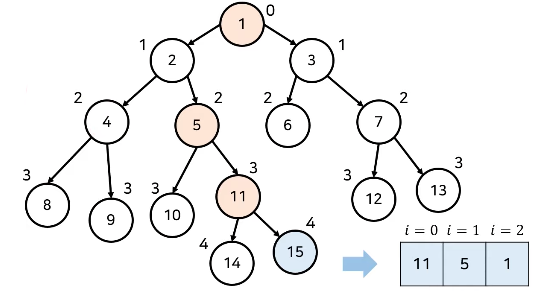
info

LCA는 오직 binary-tree에서만 사용가능 한가? NO! - 구현 링크

코드

import sys
sys.setrecursionlimit(100000) # 런타임 오류를 피하기 위한 재귀 깊이 제한 설정
input = sys.stdin.readline # 시간 초과를 피하기 위한 빠른 입력 함수
LENGTH = 21 # 2 ^ 20 = 1,000,000

n = int(input())
parent = [[0] * LENGTH for _ in range(n + 1)] # 부모 노드 정보
visited = [False] * (n + 1) # 각 노드의 깊이가 계산 되었는지의 여부
d = [0] * (n + 1) # 각 노드까지의 깊이
graph = [[] for _ in range(n + 1)] # 그래프 정보

# 양 방향 트리 만들어주기
for _ in range(n - 1):
    a, b = map(int, input().split())
    graph[a].append(b)
    graph[b].append(a)

# 루트 노드부터 시작하여 깊이를 구하는 함수
def dfs(x, depth):
    visited[x] = True
    d[x] = depth

    for node in graph[x]:
        if visited[node]: # 이미 깊이를 구했다면 넘기기
            continue
        # 우선 바로 위에 있는 부모 정보만 갱신
        parent[node][0] = x
        dfs(node, depth + 1)


# 모든 노드의 전체 부모 관계 갱신하기
def set_parent():
    dfs(1, 0) # 루트 노드는 1번 노드
    for i in range(1, LENGTH):
        for j in range(1, n + 1):
            # 각 노드에 대해 2**i번째 부모 정보 갱신
            parent[j][i] = parent[parent[j][i - 1]][i - 1]


def lca(a, b):
    # 무조건 b의 깊이가 더 깊도록 설정
    if d[a] > d[b]:
        a, b = b, a

    # a와 b의 깊이가 동일해주도록 설정
    for i in range(LENGTH - 1, -1, -1):
        if d[b] - d[a] >= 2**i:
            b = parent[b][i]

    if a == b:
        return a

    # 올라가면서 공통 조상 찾기
    for i in range(LENGTH - 1, -1, -1):
        if parent[a][i] != parent[b][i]:
            a = parent[a][i]
            b = parent[b][i]

    return parent[a][0]


set_parent()


# m개의 쿼리에 대해 lca 수행
m = int(input())

for _ in range(m):
    a, b = map(int, input().split())
    print(lca(a, b))

예제 문제

• 백준 11437번 LCA
• 백준 11438번 LCA2

나올 수 있는 면접 질문

• LCA 알고리즘이란 무엇인가요?
• LCA 구현 방법에는 어떤 것들이 있나요?
• LCA의 시간복잡도는 어떻게 되나요?
• LCA의 알고리즘이 어떻게 진행되는지 트리를 보며 설명해주세요.

참고

• LCA 알고리즘 - Crocus 블로그
• 나동빈 유튜브 강의 LCA

기여자

_{Kyun Heo}
📦